[论文学习]S²R:通过强化学习教会 LLM 自我验证和自我修正
资料
论文:[2502.12853] S$^2$R: Teaching LLMs to Self-verify and Self-correct via Reinforcement Learning
简介
本文提出了一种名为S²R的方法,以提高大型语言模型(LLMs)的推理能力。S²R 通过两阶段训练:首先,使用监督微调(SFT)让模型学习自我验证和自我纠正的行为;然后,通过基于强化学习(RL)的优化进一步增强这些能力。实验表明,即使在训练数据有限的情况下,S²R 也能显著提升 LLMs 在数学推理任务中的表现,优于仅使用长链思维(CoT)训练的数据集。研究还发现,自验证和自纠正能力不仅适用于数学推理,还可泛化至其他任务,如逻辑推理和代码理解。此外,论文比较了过程级和结果级强化学习的效果,并探讨了离线 RL 作为更高效的训练替代方案的可行性。
相关工作
缩放测试时间计算
人们越来越关注训练LLMs自己执行测试时间搜索,通常通过进行更长和更深入的思考。这些测试时间缩放工作不仅直接有益于LLM重建,而且还可以集成回训练时间,从而实现LLM重建的迭代改进 。而在这项工作中,文章提出了一个有效的框架,用于训练LLMs通过自我验证和自我纠正来进行有效的测试时间扩展。这种方法无需付出大量努力即可实现,并且S2R的性能也可以通过迭代训练得到持续提升。
自我验证和自我纠正
使LLMs能够执行有效的自我验证和自我纠正是实现LLMs健壮推理的有前途的解决方案 ,这些能力对于执行深度推理也至关重要。先前的研究表明,在大多数情况下,直接提示LLMs进行自我验证或自我纠正是不理想的 。而文章提出了一种通过原理性的模仿数据构建和RL训练来增强LLMs的自我验证和自我纠正能力的有效方法,并通过深入分析证明了该方法的有效性。
RL用于LLM Reasoning
强化学习已被证明在提高各种任务的LLM性能方面是有效的。在LLM推理中,先前的研究通常将RL用于actor-critic框架中 ,而为RL训练开发准确奖励模型的研究一直是一个长期的目标,特别是在过程级RL的奖励模型方面 。而最近研究表明,简化的奖励建模和优势估计在RL训练中也可以有效地增强LLM推理能力。在这项工作中,我们还表明,简化的优势估计和RL框架可以有效地改进LLM推理。并且文章还对过程级RL、结果级RL和离线RL进行了分析,为未来lm推理的RL工作提供了见解。
方法
S²R 主要由两个阶段组成:
PS:阶段0是指数据的构建。
- 行为初始化:使用监督微调(SFT)在 carefully curated 数据上训练模型,使其掌握初步的自我验证和自我纠正能力。
- 强化学习优化:结合结果级和过程级强化学习,使模型在推理过程中不断优化自己的推理路径。
S²R 采用的关键策略:
- 自我验证:模型在推理过程中检查自己的答案是否正确。
- 自我纠正:模型在发现错误后,自主改正答案。
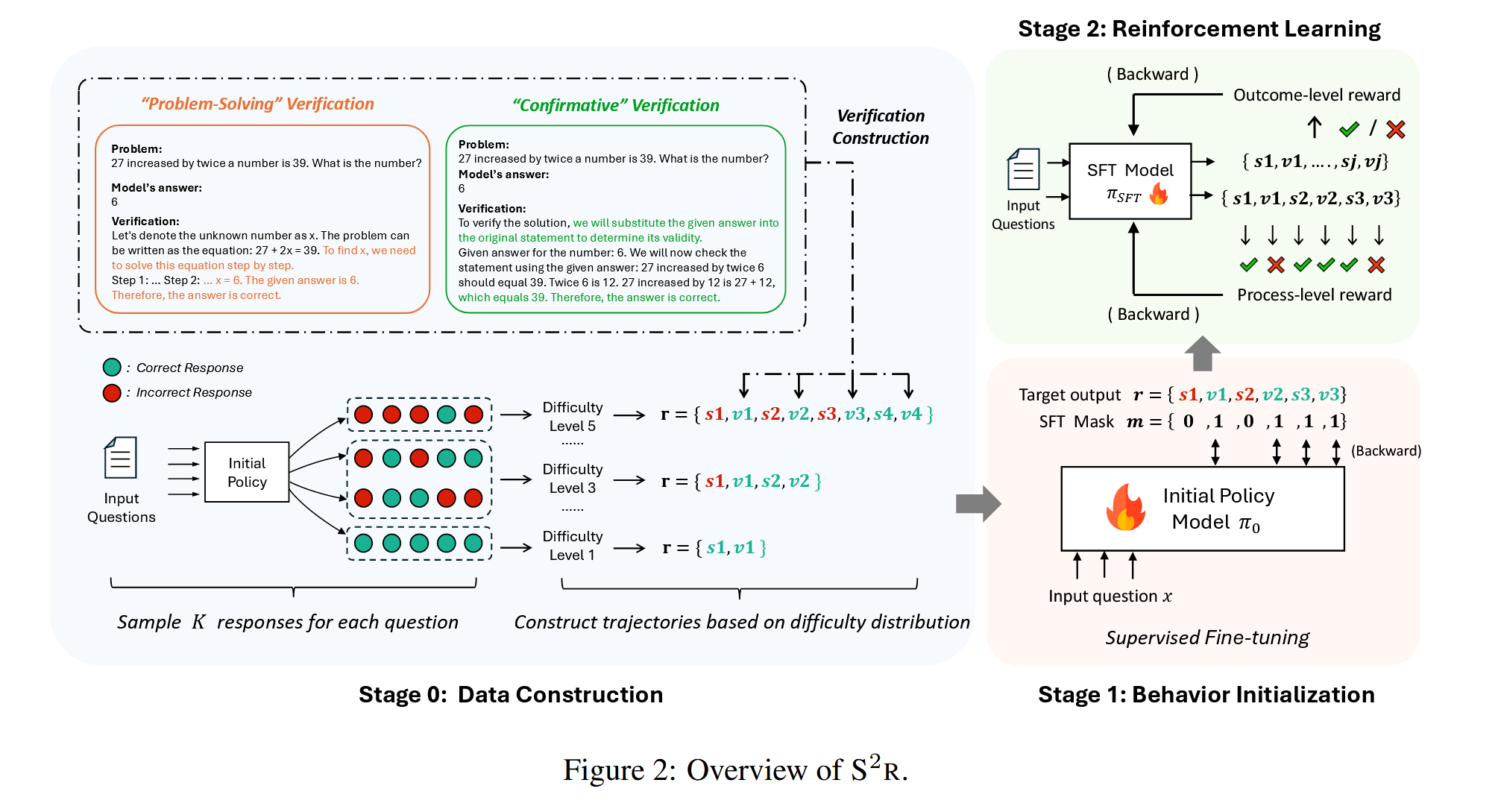
自我验证和自我纠正行为的初始化
自我验证
- 问题求解型验证:通过重新求解问题来验证答案。“问题解决式”验证直观上并非所期望的理想验证行为。
- 确认型验证:通过替代方法验证答案的正确性。理想情况下,希望模型能够跳出固有思维模式,从新的视角重新审视解决方案,而非仅仅思考 从同样的问题解决视角进行验证。通过提示现有的大型语言模型“在不 重新解决问题的情况下验证答案的正确性”来 构建“确认式”验证,并使用大型语言模型作为裁判来过滤掉无效的验证。
自我纠正
LLMs通常无法通过SFT学习有效的自我纠正行为,但自我纠正的有效性可以通过强化学习来增强。只在这个阶段初始化自我纠正行为,将进一步增强自我纠正能力的工作留给RL阶段。
构建动态试错轨迹
- 为了确保轨迹的多样性,构建各种长度的轨迹。
- 为了确保LLMs学会验证和纠正自己的错误,我们通过从LLMs的响应中进行抽样和筛选来构建每个轨迹中的失败试验。
- 合理的测试时间缩放方法将合理的工作分配给不同级别的问题,具体来说,在达到正确答案之前,更困难的问题需要更多的试错迭代次数。因此根据每个基础模型采样响应的准确性来确定每条轨迹的长度。
监督微调以初始化思维行为

在训练过程中,通过使用掩码来优化所有验证的概率,而仅对最后一个正确 的解 $s_N$进行优化。
通过强化学习提升思维能力
结果级强化学习RLOO
- 目标是提升最终答案的正确率。
- 适合较强的 LLMs,如 Qwen2.5-Math-7B。
结果级强化学习(RLOO,REINFORCE Leave-One-Out)是一种基于最终结果的强化学习方法。它通过评估最终答案的正确性来优化模型的行为轨迹。具体而言:
- 奖励函数:基于最终答案的正确性,正确答案获得正奖励(+1),错误答案获得负奖励(-1)。
- 优势估计:通过留一法(Leave-One-Out)估计基线,计算每个轨迹的优势值。
- 优化目标:通过最小化损失函数,优化整个轨迹的生成概率,鼓励模型探索更有效的推理路径。
结果级强化学习的优势在于允许模型在中间步骤中自由探索,最终优化最终答案的正确性。
过程级组强化学习
- 目标是优化推理过程的每一步。
- 适用于推理能力较弱的 LLMs,如 Qwen2-7B-Instruct。
过程级强化学习关注推理过程中的每个步骤,通过为每个动作(如“验证”或“解决”)分配奖励来优化模型的行为。具体方法如下:
- 奖励函数:根据动作类型(验证或解决)和动作的正确性分配奖励。例如,正确的解决动作获得+1奖励,错误的验证动作获得-1奖励。
- 基线估计:通过组内动作的平均奖励估计基线,确保相同奖励上下文的动作具有相似的基线。
- 优化目标:通过最小化每个动作的损失函数,优化模型在每个步骤的行为。
过程级强化学习的优势在于能够直接优化中间步骤的正确性,适合推理能力较弱的模型。
更高效的离线强化学习
离线强化学习是一种更高效的替代方案,能够在计算资源受限的情况下提供类似的性能提升。不依赖实时采样的强化学习方法,具有更高的效率和更稳定的训练过程。本文探索了离线强化学习在S2R框架中的应用:
- 准确性分组基线:通过问题的难度(通过准确率估计)对轨迹进行分组,进一步优化基线估计。
- 损失函数:结合准确性分组和位置信息,计算每个动作的优势值,并优化模型的行为。
- 实施细节:通过过滤、采样和优化步骤,离线强化学习能够在大规模数据上高效训练,减少计算资源的消耗。
离线强化学习的优势在于能够利用大规模数据进行更准确的基线估计,同时避免了在线强化学习中的实时采样开销。
实验
实验设置
实验数据集
在7个不同的数学基准上评估了所提出的方法。为确保进行全面的评估,此外,还使用了分布式GSM8K和MATH500测试集,包括具有挑战性的分配外基准,涵盖各种难度级别和数学领域,包括AIME 2024竞争问题,AMC2023考试,来自奥林匹克长凳的高级rea-soning任务 ,以及大学数学的大学级问题集。此外,还评估了在真实世界标准化测试中的表现,即高考。
实验模型
使用三种不同的基础模型加以S²R框架进行实验:
- Llama-3.1-8B-Instruct
- qwen2-7B-Instruct
- Qwen2.5-Math-7B
其中Llama-3.1-8B-Instruct和Qwen2-7B-Instruct是在不同领域进行训练的通用模型。Qwen2.5-Math-7B是专门为数学问题解决而定制的最先进模型。
提出的方法与四类强基准模型进行比较:
- Frontier LLMs:包括前沿的专有模型,如GPT-4o、最新的Claude以及OpenAI的o1-preview和o1-mini。
- 顶级开源推理模型:涵盖以强大的推理能力而闻名的最先进的开源模型,包括Mathstral-7B-v0.1,NuminaMath-72B,LLaMA3.1-70B-Instruct和Qwen2.5-Math-72B-Instruct。
- 基于Qwen2.5-Math-7B的增强模型: 鉴于最近Qwen2.5-Math-7B作为基础模型的流行,我们根据Qwen2.5-Math-7B的三个竞争基线(Eurus-2-7B-PRIME,rStar-Math-7B。和Qwen2.5-7b-implerl)评估S²R,这些模块作为我们的Qwen2.5-Math-7B-based变体的直接和强有力的基准。
- 具有不同CoT结构的SFT: 还比较了竞争性类型的CoT推理的训练,包括训练数据集中的原始CoT解决方案,和从广泛采用的开源o1-like模型 “QwQ-32B-Preview” 中提炼出来的Long-ccosso-lutions。
实验结果
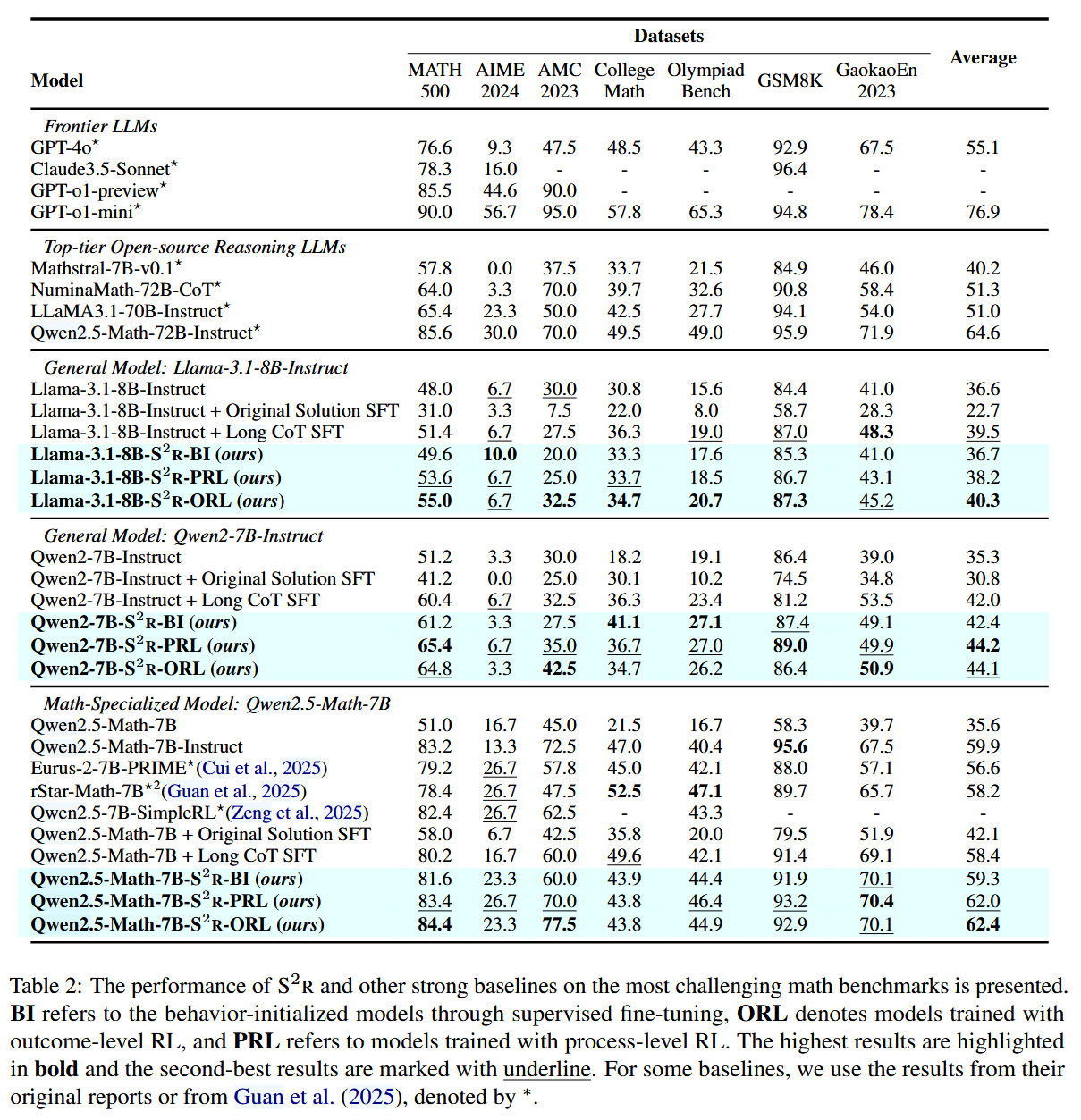
论文在多个数学推理基准数据集(如 MATH500, GSM8K)上测试了 S²R,主要结果如下:
- S²R 在 Qwen2.5-Math-7B 上的准确率从 51.0% 提高到 81.6%,超越了等量的长链思维(CoT)数据微调模型(80.2%)。
- 过程级强化学习(Process-level RL)更适用于初始推理能力较弱的模型,而结果级强化学习(Outcome-level RL)更能提升较强模型的推理能力。
- S²R 泛化能力强,在跨领域任务(如逻辑推理、代码推理)中也表现良好。
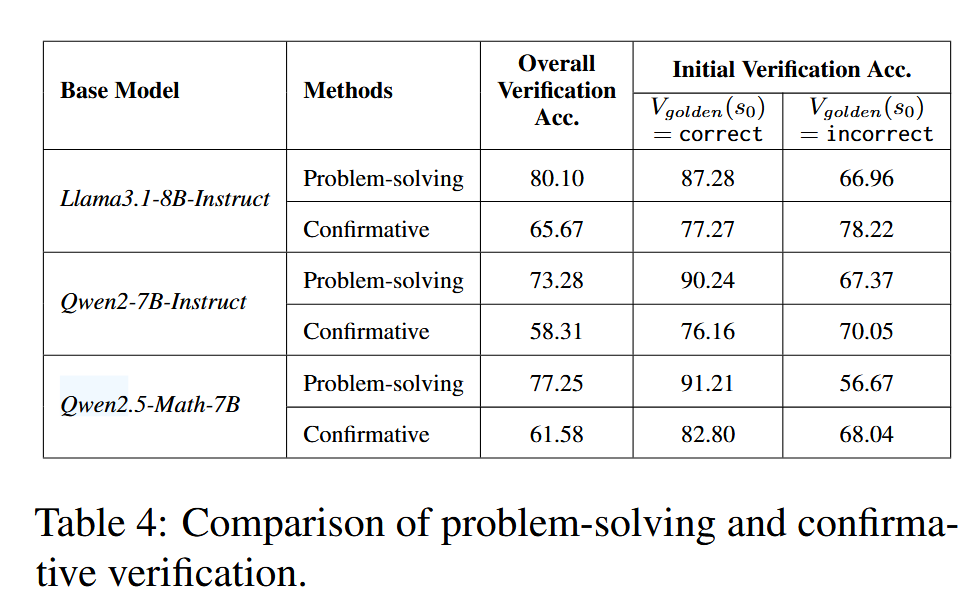
分析自我验证和自我纠正能力
首先对问题解决法和确认性验证法进行比较。如图表格展示 了不同方法在 Math500 测试集上的验证结果。 其指出总体而言,问题解决验证的总体准确率通常优于确认性验证。之后在所有实验中,都使用了确认性验证来进行行为初始化。
之后研究强化学习训练对模型自我验证和自我修正能力的影响。如图中,我们展示了行为初始化模型 (SFT)以及从 Qwen2.5-Math-7B 获得的不同强化学习模型的结果。
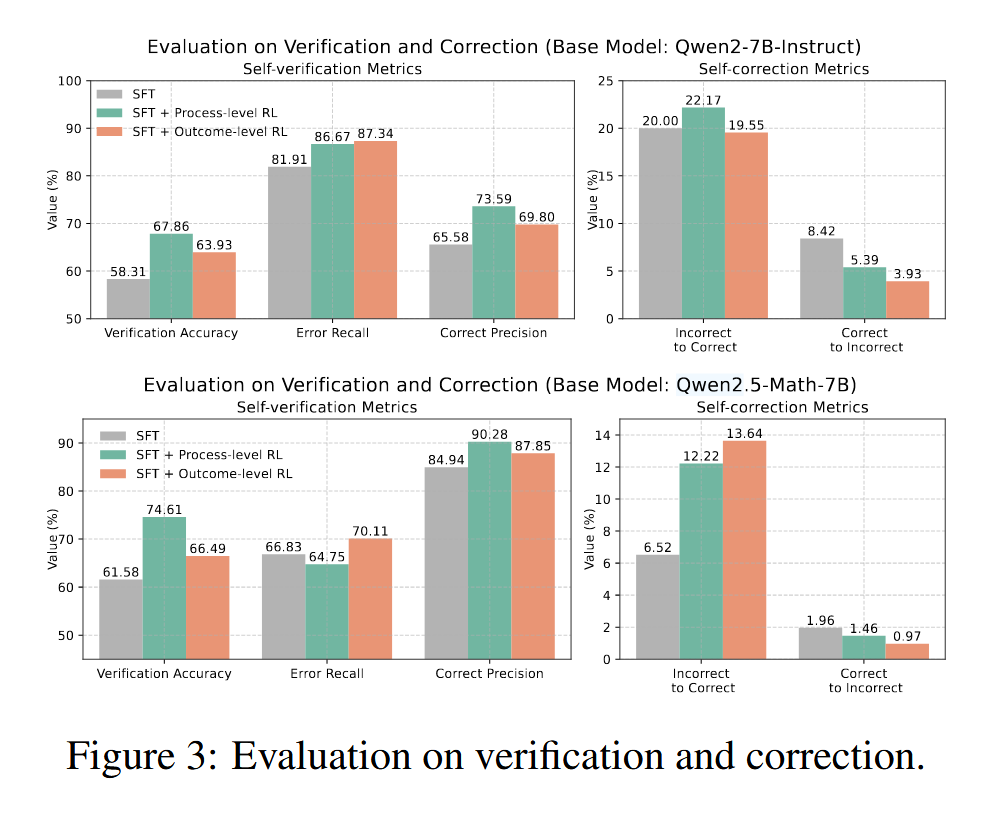
- 两种强化学习方法均能有效提高自我验证的准确 性。过程级强化学习在准确性方面表现出更大 的提升,而结果级强化学习则持续提高了错误 召回率和正确精度。这可能是因为过程级监督不加区分地促进了中间步骤的验证准确性,而 结果级监督允许策略模型在中间步骤自由探索, 仅提升最终答案的准确性,从而主要增强了错误召回率和正确精度。
- 两种强化学习方法都能成功提升模型的自我纠正能力。值得注意的是, 经过强化学习训练后,模型纠正错误答案的能 力显著提高,模型错误修改正确答案的比率也 显著降低。这一比较表明,S2R 能够显著增强 模型自我纠正能力的有效性。
之后为了进一步说明 S2R 训练的效果,如图展示了 SFT 和 SFT+RL 模型在不同难度水平下的答案准确率和平均试验次数。
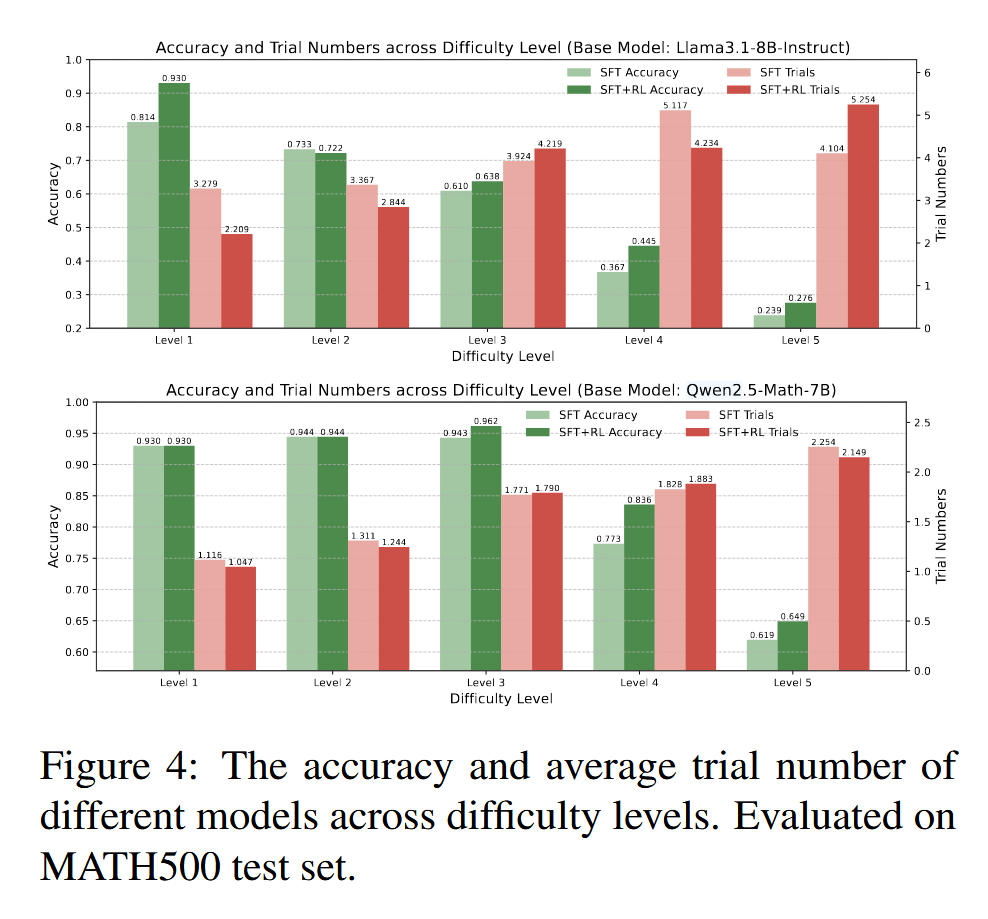
- 通过在推理过程中学习自我验证和自我纠正,模型学会了动态分配测试时的努力。对于较容易的问题,模型可以用较少的试验次数得出有把握的 答案,而对于较难的问题,则需要更多的试验次 数才能得出有把握的答案。
- 强化学习进一步改善了测试时的努力分配,特别是对于能力较弱的模型。
- 经 过强化学习训练后,较难问题的答案准确率显著提高,这表明自我验证和自我纠正范式在增强模型推理能力方面是有效的。
总结
S²R 提供了一种高效的 LLMs 训练范式,使模型能够在推理过程中自主检查和优化自己的答案,不仅提升了数学推理能力,还能泛化到其他任务。通过在 多个数学推理基准数据集上的实验,S²R 展现出显著的推理能力提升,同时在逻辑推理、代码推理等跨领域任务中也表现优异。其创新性在于结合监督微调(SFT)和强化学习(RL)优化,使得 LLM 能够在有限的资源下高效学习自我验证和自我纠正策略,进而提升推理的准确性和稳定性。未来,S²R 可进一步扩展至更多复杂推理任务,如科学研究、医学诊断等,推动 LLM 在更广泛场景中的应用。


